LiNeS

Pre-trained models excel at many tasks, but fine-tuning can lead to catastrophic forgetting, where gains on one task cause a loss in generalization. We introduce LiNeS (Layer-Increasing Network Scaling), a post-fine-tuning method that preserves general knowledge in shallow layers while allowing deeper layers to specialize. This helps models retain both task-specific improvements and their ability to generalize.

LiNeS also shines in multi-task model merging, reducing interference between tasks and boosting performance across both vision and language benchmarks. It enhances models in out-of-distribution scenarios and improves the merging of language models fine-tuned with different reward signals. LiNeS is simple to implement and integrates seamlessly with existing methods.

Post-training Layer-wise Scaling Mitigates Forgetting

The key insight behind our method is that scaling down the updates to shallow layers after fine-tuning can help mitigate catastrophic forgetting. This way, the model preserves its ability to generalize while still performing well on the specific task it was fine-tuned for. Let's walk through how this works.

Fine-tuning and Forgetting

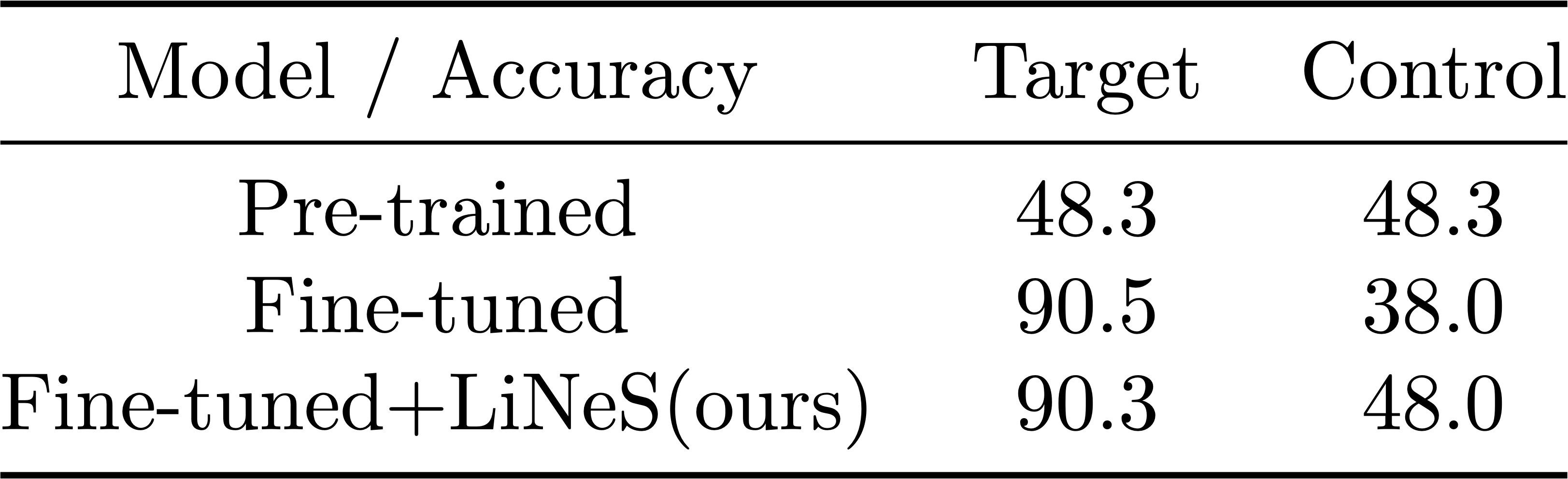
First, we demonstrate the problem of catastrophic forgetting. Using the CLIP ViT-B/32 model, we fine-tuned it on an 8-task image classification benchmark. We measured the model's performance on both the target task (the one we fine-tuned on) and the remaining 7 control tasks. As we see on the right, fine-tuning boosts performance on the target task but causes a steep drop in accuracy on the control tasks. This shows how much generalization is lost after fine-tuning.

Shallow Layers vs. Deeper Layers

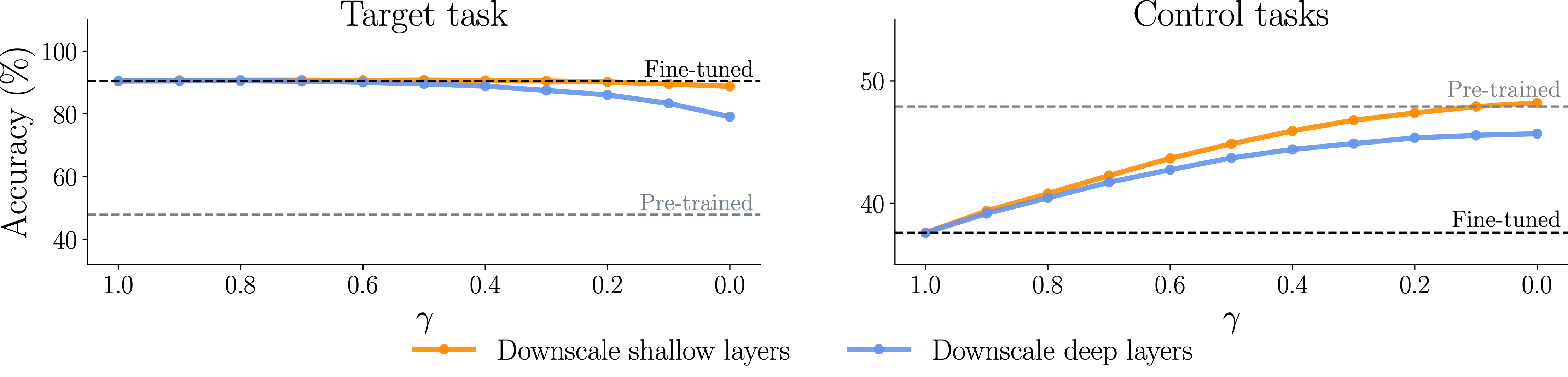
Most of the updates that happen during fine-tuning are actually unnecessary for maintaining target task accuracy. Prior work shows that the deeper layers are more important for task-specific features, while shallow layers hold general features. Based on this, we hypothesized that scaling down the updates to shallow layers after fine-tuning could preserve generalization without sacrificing target task performance.

In our experiment, we applied a linearly increasing scaling schedule that reduces updates to shallow layers while leaving deeper layers more or less unchanged. Specifically, layer \ell is multiplied by a scaling factor: $$ \lambda^{(\ell)}= \gamma + (1-\gamma) \frac{\ell-1}{L-1}, \quad \forall \ell \in[L]. $$

As shown in below, even with aggressive downscaling of shallow layers, the target task accuracy stayed nearly the same. However, when we downscaled the deeper layers, performance dropped sharply. This supports our idea that shallow-layer updates don't contribute much to the target task's success.

Shallow-layer Updates Hurt Generalization

While shallow-layer updates have a minimal impact on the target task, they do impact the model's generalization ability. These layers hold general features learned during pre-training, and updating them during fine-tuning can distort these features. By downscaling the updates to the shallow layers, we found that we could restore much of the zero-shot generalization lost during fine-tuning, as seen in the right side of the figure above. The control tasks' accuracy almost returned to the level of the pre-trained model.

Striking the Right Balance

To strike the best balance between target task accuracy and generalization on control tasks, we optimized the scaling coefficient for each model. As we saw on the first table, our method leads to minimal loss in target task accuracy (only a 0.2% drop) but restores a full 10% improvement in control task performance. We also applied this approach to a larger 20-task benchmark, and the results, illustrated in the figure on the right, show that LiNeS maintains strong target task accuracy (99.8%) while also significantly improving control task generalization (97.9%).

LiNeS mitigates forgetting while preserving target task performance.

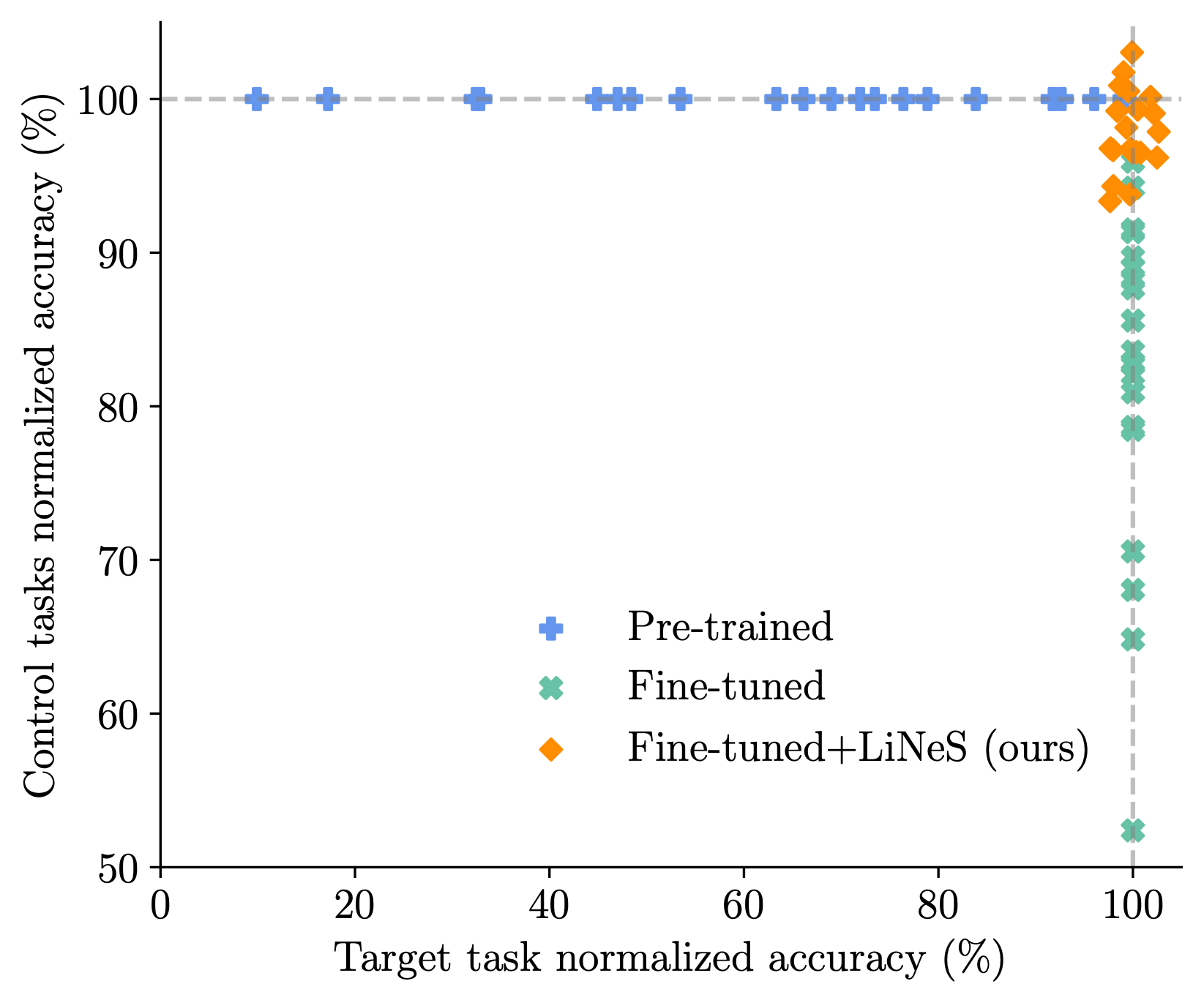
By carefully downscaling shallow layers, we're able to prevent catastrophic forgetting and preserve the generalization powers of pre-trained models while fine-tuning them for specific tasks.

Method

All these insights led us to a pretty straightforward solution: LiNeS (Layer-Increasing Network Scaling). The idea is simple—different layers in the model need different amounts of fine-tuning. Shallow layers should stay close to their original pre-trained state since they hold general knowledge, while deeper layers can be adapted more to the specific task.

So how do we do this? We scale the updates differently for each layer based on how deep it is. We keep shallow layers mostly unchanged, but let deeper layers adapt more. This way, we can fine-tune the model without it forgetting everything it learned before.

Here's how it works in a nutshell: $$ \boldsymbol{\tau}_{\textrm{LiNeS}} = \texttt{concat}(\lambda^{(1)} {\boldsymbol{\tau}}^{(1)}, ..., \lambda^{(L)} \boldsymbol{\tau}^{(L)} ), \text{ where } \lambda^{(\ell)} = \alpha + \beta \frac{\ell-1}{L-1} , \quad \forall \ell \in [L] $$

This formula adjusts the updates from shallow layers (small scaling with \alpha) to deep layers (larger scaling with \alpha+\beta ). In simple terms, the deeper the layer, the more it's fine-tuned. Shallow layers? Barely touched.

In our experiments we only adjust one of the hyperparameters and use heuristics to set the other. LiNeS isflexible and easy to tune for different needs, whether you're working with a single task or merging models across multiple tasks.

We'll dive into more detail on how we tuned these parameters in our experiments, but the core idea remains simple: adjust the fine-tuning for each layer based on how deep it is, and you get the best of both worlds—great performance on the task at hand, without sacrificing generalization.

Experiments

Improving Robust Fine-tuning for OOD Generalization

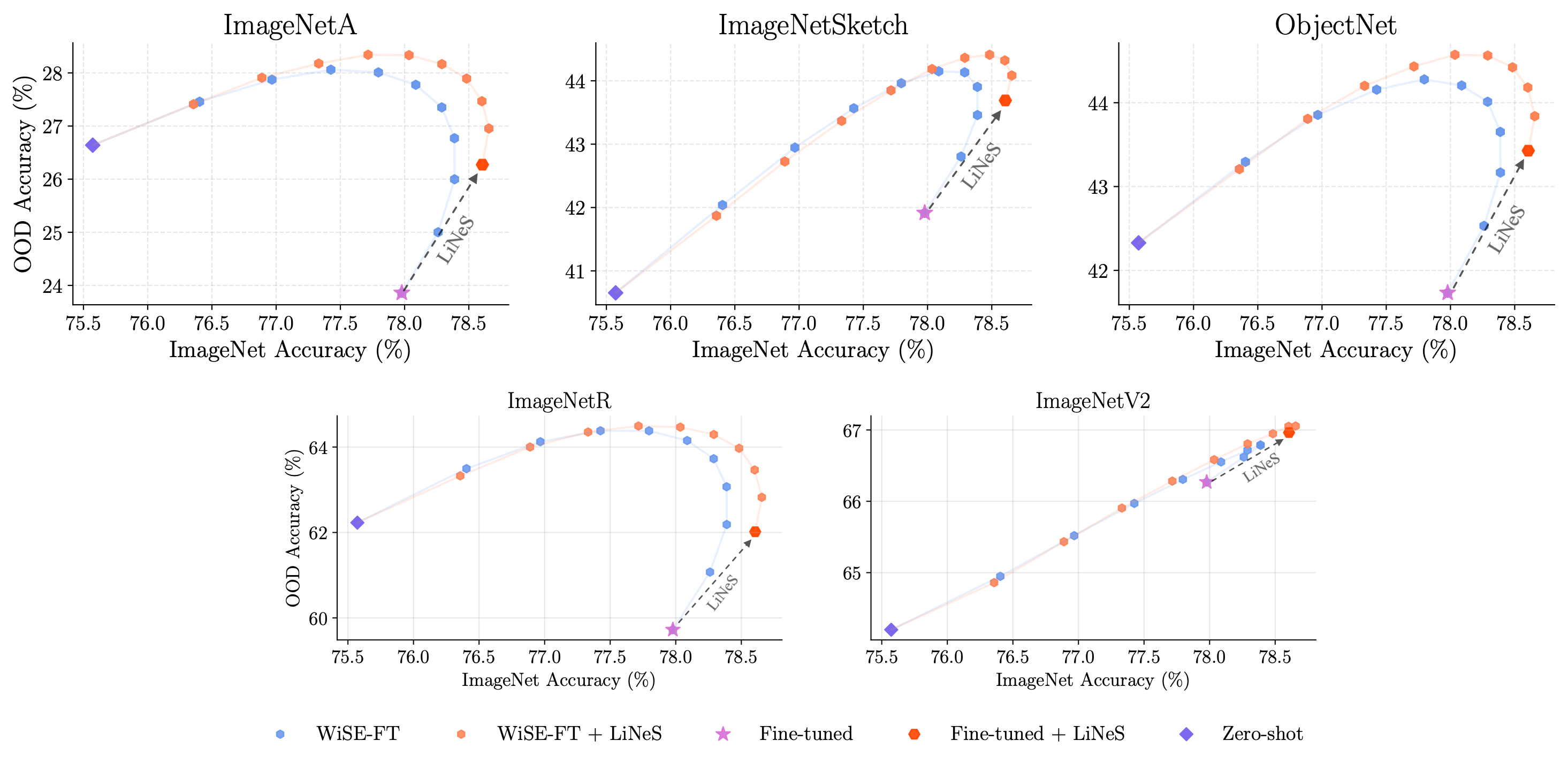
We next evaluated the effectiveness of LiNeS in the context of Out-of-Distribution (OOD) generalization, where models encounter data that significantly differs from their training set. A widely used method for this scenario is WiSE-FT (Weight Interpolation for Stronger Fine-tuning) , which interpolates between pre-trained and fine-tuned model weights to enhance performance on OOD datasets. The interpolation can be formulated as a combination of the pre-trained weights ( \theta_0 ) and the fine-tuned updates ( \tau ), controlled by a parameter \gamma , as follows: (1 - \gamma) \theta_0 + \gamma \theta = \theta_0 + \gamma \tau . This method allows the model to retain its pre-trained knowledge while benefiting from task-specific fine-tuning.

To assess the impact of LiNeS, we applied it to this interpolation process using CLIP models fine-tuned on ImageNet. We evaluated performance across five OOD datasets: ImageNetSketch, ImageNet-A, ImageNet-R, ObjectNet, and ImageNet-V2. We experimented with 70 fine-tuned checkpoints, applying LiNeS with \alpha = \beta = 0.5 . Even without applying WiSE-FT, LiNeS substantially improved both in-distribution (ID) and OOD performance. When LiNeS was combined with WiSE-FT, the performance gains were even more pronounced. As we see below, the resulting Pareto Front consistently dominated that of WiSE-FT across all distribution shifts, demonstrating the robustness of LiNeS under various conditions. Overall, LiNeS complements WiSE-FT by providing a scalable and efficient method for robust fine-tuning in diverse environments.

Improving Multi-task Model Merging

We can also extend LiNeS to enhance multi-task model merging algorithms, allowing for the integration of multiple models fine-tuned on different tasks into a single robust model. The intuition behind this approach is to mitigate task interference, which often occurs when merging individual task vectors—this interference can degrade overall performance due to the conflicting contributions of different tasks.

To evaluate the effectiveness of our method, we apply LiNeS to various merging techniques, including Task Arithmetic , Ties-Merging , and Consensus Merging , across several benchmarks in both computer vision and natural language processing.

Computer Vision

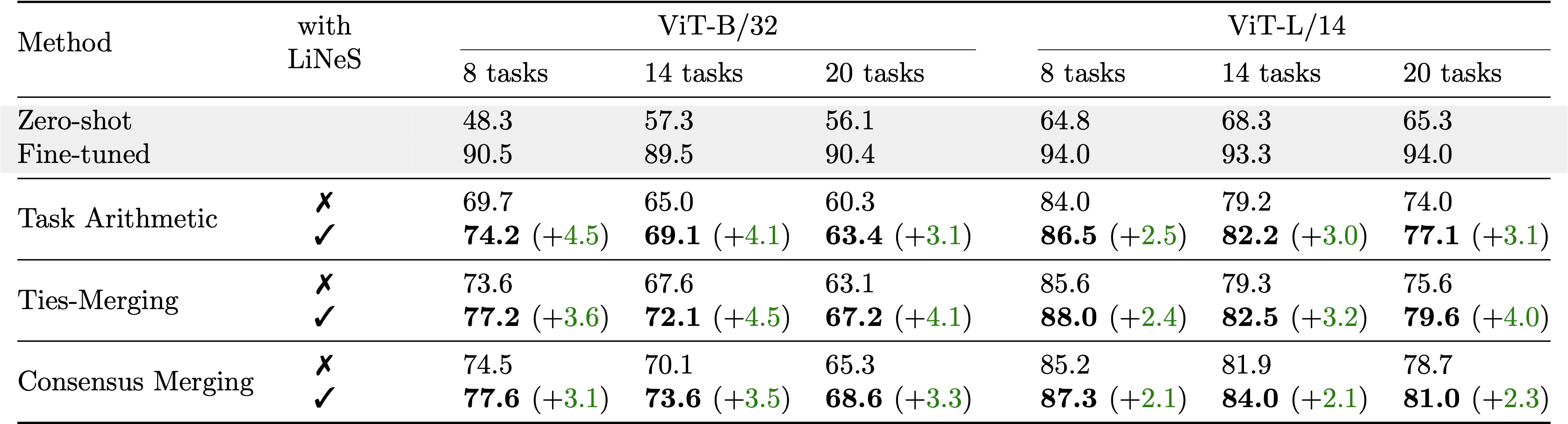
We conducted experiments using the 8-task, 14-task, and 20-task benchmarks to assess the performance of our method. As shown in below, LiNeS significantly boosts performance across all merging strategies and model sizes.

Natural Language Processing

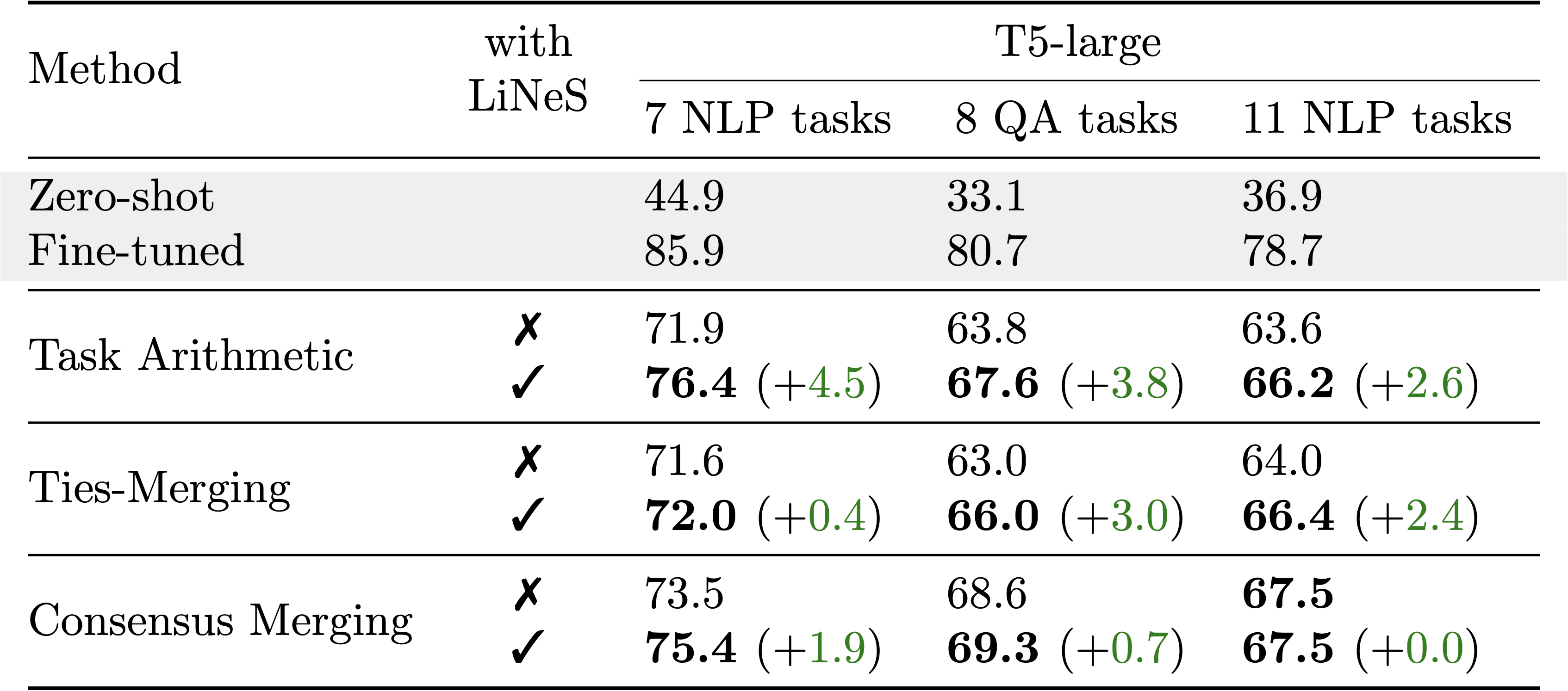
We also evaluated LiNeS in the NLP domain, focusing on various benchmarks, including 7-task NLP and 8-task Question-Answering tasks, as well as their 11-task union. Our results indicate that LiNeS enhances multi-task performance across all tested baseline methods, affirming its versatility and robustness in both computer vision and NLP applications.

Improving Model Soups for Merging Single-task Models

Averaging multiple models fine-tuned on the same task can enhance performance, as demonstrated in the Model Soups framework . We investigate whether LiNeS can further improve test performance when merging single-task models. Merging 70 CLIP ViT-B/32 checkpoints fine-tuned on ImageNet, we apply LiNeS to the weight averaging process, tuning the parameter \beta while fixing \alpha = 1 . Our results on the right show that LiNeS outperforms both vanilla soups and task arithmetic, achieving improvements of 0.48% and 0.15% on ImageNet for uniform and greedy soup methods, respectively. These findings demonstrate that LiNeS effectively enhances the merging of single-task models, yielding the best-performing configurations by leveraging the gains from greedy soup. This reinforces the utility of LiNeS in optimizing model performance across various merging strategies.

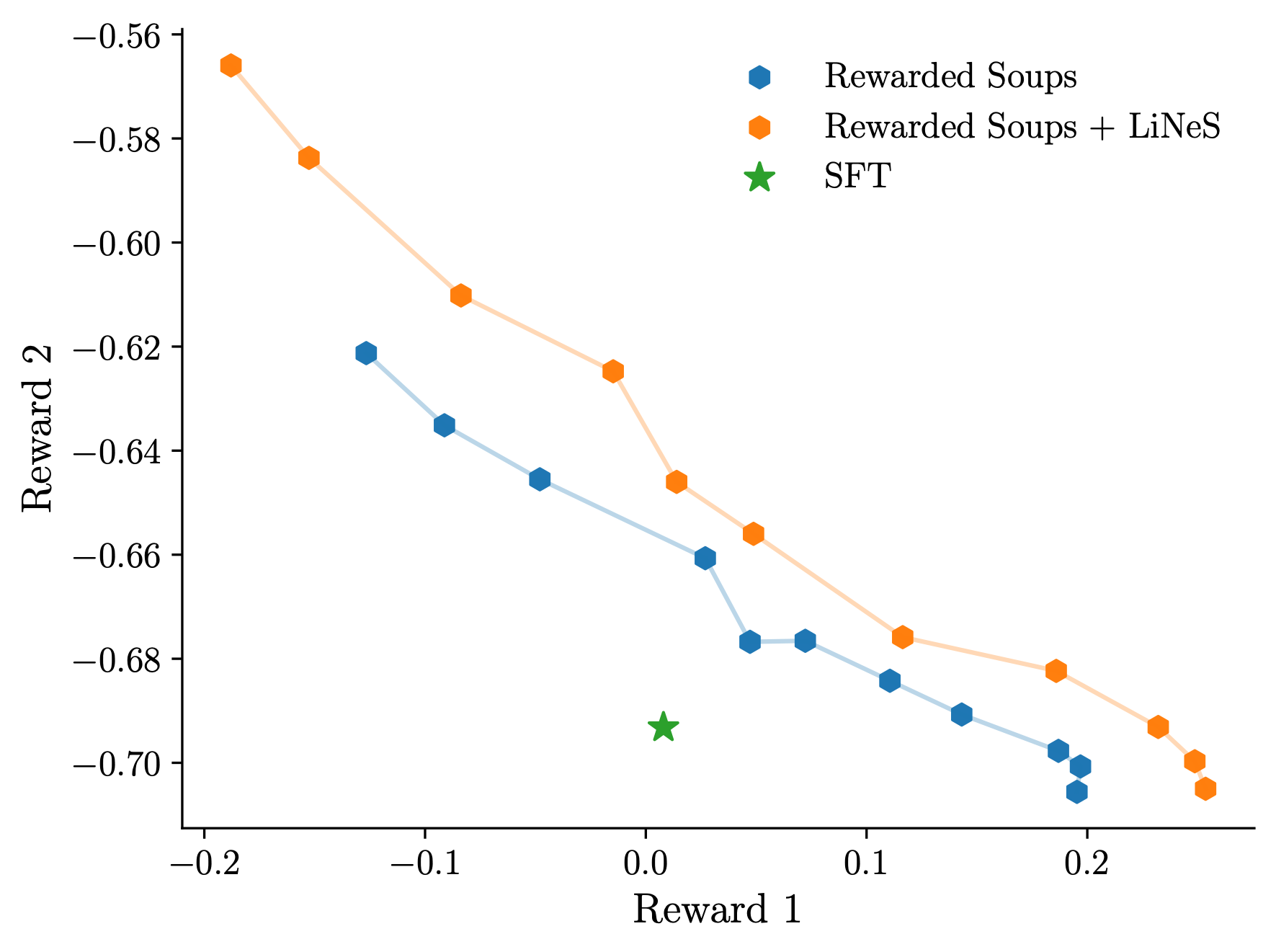
Improving Rewarded Soups

We investigate the effectiveness of LiNeS for merging foundation models fine-tuned on different rewards, following the Rewarded Soups framework . This method interpolates the weights {\theta}_1 and {\theta}_2 of two LLM policies optimized for distinct rewards R_1 and R_2 . Starting with an LLM parameterized by {\theta}_0 , we fine-tune it using supervised fine-tuning (SFT) on labeled demonstrations. Following SFT, we apply Reinforcement Learning from Human Feedback (RLHF) , to train two policies using Proximal Policy Optimization (PPO) . The merging of these policies is expressed as:

$$ \boldsymbol{\theta}_{RS} = \boldsymbol{\theta}_{SFT} + \lambda \boldsymbol{\tau}_1 + (1-\lambda) \boldsymbol{\tau}_2, \quad \lambda \in [0,1], $$

We apply LiNeS to the weighted-sum residual \lambda \tau_1 + (1-\lambda) \tau_2 , fixing \alpha = \beta = 1 for computational efficiency. In our experiments, we use the LLaMA-2 7B model and the Reddit Summary task , employing two reward models to evaluate performance. As we see on the right, LiNeS consistently outperforms vanilla Rewarded Soups across the full preference space, achieving a dominating Pareto Front and demonstrating its general applicability in enhancing the merging of LLM policies fine-tuned on different rewards.

Final remarks

In this work, we introduced LiNeS, a novel method aimed at mitigating catastrophic forgetting during fine-tuning. By reducing the magnitude of parameter updates in shallow layers, LiNeS enhances generalization on control tasks while preserving performance on fine-tuned tasks. We demonstrated the versatility of LiNeS in tackling task interference during multi-task model merging, consistently improving baseline merging methods across both vision and NLP benchmarks. Our experiments validated the broad applicability of LiNeS, from enhancing OOD generalization to improving single-task and multi-task model merging, as well as merging LLM policies optimized for different rewards. Given its simplicity and ease of integration, LiNeS provides a practical and efficient solution for improving the generalization and robustness of fine-tuned models across diverse applications.